Cononical vine (C-vine). More...

Inheritance diagram for starvine.vine.C_vine.Cvine:

Public Member Functions
def	__init__ (self, data, dataWeights=None)

def	constructVine (self)
	Sequentially construct the vine structure. More...

def	buildDeepTrees (self, level=1)
	Recursivley build each tree in the vine. More...

Public Member Functions inherited from starvine.vine.base_vine.BaseVine
def	__init__ (self, data=None, weights=None)

def	loadVineStructure (self, vS)
	Load saved vine structure.

def	vineNLLH (self, vineParams=[None], kwargs)
	Compute the vine negative log likelyhood. More...

def	sfitMLE (self, kwargs)
	Simulataneously estimate all copula paramters in the vine by MLE. More...

def	treeHfun (self, level=0)
	Operates on a tree, T_(i). More...

def	sample (self, n=1000)
	Draws n samples from the vine. More...

def	plotVine (self, plotAll=True, savefig=None)
	Plots the vine's graph structure. More...

Public Attributes
	data

	weights

	nLevels

	vine

Public Attributes inherited from starvine.vine.base_vine.BaseVine
	nLLH

	vineParams

	vineParamsMap

	fittedParams

Detailed Description

Cononical vine (C-vine).

Provides methods to fit pair copula constructions sequentially and simultaneously. Additional methods are provided to draw samples from a constructed C-vine. Base class starvine.vine.base_vine.BaseVine .

Example 3 variable C-vine structure:

Tree level 1

X1 ---C_13--- X3
|
C_12
|
X2

Tree level 2

F(X2|X1) ---C_23|1--- F(X3|X1)

The nodes of the top level tree are the rank transformed, uniformly distributed marginals (defined on [0, 1]).

The formation of the lower level trees involve computing conditional distributions of the form:

$F(x|v)$

For the bivariate case, Joe (1996) showed that:

$F(x|v) = \frac{\partial C_{x,v}(F(x), F(v))}{\partial F_v(v)}$

Which simplifies further if x and v are uniform:

$h(x| v, \theta) = F(x|v, \theta) = \frac{\partial C_{xv}(x,v,\theta)}{\partial v}$

Where we have defined the convinience conditional distribution 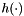$h(\cdot)$

The nodes of the lower level trees are formed by using 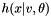$h(x| v,\theta)$ to compute marginal distirbution of the RV 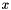$ x $ given the parent copula's parameters 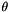$\theta$ and the root node's uniformly distributed $ v $ .

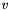The n-dimensional density of a C-vine copula is given by:

$\prod_{k=1}^n f(x_k) \prod_{j=1}^{n-1} \prod_{i=1}^{n-j} c_{j,j+i|1,...j-1} (F(x_j|x_1...,x_{j-1}), F(x_{j+1}|x_1...,x_{j-1}))$

Where the outer product index represents the tree level, and the inner product indicies represent the pair copula constructions (PCC) withen the given tree.

Member Function Documentation

§ buildDeepTrees()

def starvine.vine.C_vine.Cvine.buildDeepTrees	(	self,
		level = `1`
	)

Recursivley build each tree in the vine.

Must keep track of edge—node linkages between trees.

Parameters

level int Current tree level.

§ constructVine()

def starvine.vine.C_vine.Cvine.constructVine ( self )

Sequentially construct the vine structure.

Construct the top-level tree first, then recursively build all tree levels.

The documentation for this class was generated from the following file:

starvine/vine/C_vine.py